EHTG Talk – Uncertainty Quantification in Oncology • Alexander Zeilmann

Why mathematical modeling in oncology?

Before we start discussing uncertainty quantification as a branch of mathematical oncology, let us first look at mathematical modeling in general. So what is mathematical modeling all about?

As a clinician you often have a variety of medical data for each patient and need to find an appropriate treatment or an prediction for the progress of the disease.

Now mathematical modeling can help with this task. Depending on the medical question and the available data and knowledge, we mathematicians develop mathematical models, that try to answer them.

Uncertainty in medical data can arise due to many reasons

Now I am pretty sure you are also familiar with the situation where most if not all the medical data are somewhat uncertain.

This data uncertainty can come from a variety of sources. For example: some data cannot be measured precisely or there are no direct measurements possible for financial, biomedical or ethical reasons. There might be uncertainties due to different evaluating clinicians or old measurements. Fast changing parameters can also be interpreted as uncertain and similar to this temporal heterogeneity we have a spatial heterogeneity in tissue and tumors in particular.

Yesterday, in the patient advocacy talks we have heard, that patients want to have a reduced uncertainty in screening, diagnosis and treatment. But how do we reduce the uncertainty in clinical decision making when the medical data is inherently uncertain? I strongly believe, that the best way to reduce uncertainties is to understand and quantify these uncertainties first.

Uncertainty quantification as a means to quantify uncertainties

Accordingly, medical decision making also has to consider the uncertainties of the medical data currently available.

On the other hand, the uncertainty in clinical decision making can come in many shapes. You might be very certain on some aspects, but rather uncertain on others. Or you can rule out a treatment method definitively but cannot decide between others.

You probably have a gut feeling on how certain your decisions are based on the uncertainty of the data. The good news are that mathematical modeling can also be used to describe this process. There is a field in mathematics called uncertainty quantification that can describe the uncertainty in medical data and model their influence on the uncertain medical decision.

The three pathway hypothesis of Lynch syndrome colorectal carcinogenesis

Let us consider an example: Probably all of you are familiar with Lynch syndrome colorectal cancers. For them, it is currently hypothesized that carcinogenesis comes in three different distinct pathways (Ahadova et al., 2018). Interestingly, the optimal prevention and treatment is different for the three pathways, making a characterization of them vital. The current hypothesis is that the pathway taken depends on the type and order of the involved mutations.

A Kronecker model for Lynch syndrome carcinogenesis

To this end we developed a mathematical model (Haupt et al., 2021) to estimate the number of colonic crypts with a certain mutational signature for each point in the life of a Lynch syndrome patient. The model is formulated as system of linear ordinary differential equations

\begin{align*} \dot{x} &= (A + B + C + D + E + F) x, \\ x(0) &= x_0. \end{align*}

An exact description of the model is unimportant right now, I refer the interested reader to our paper (Haupt et al., 2021) and a blog post by Saskia Haupt. The important concept is that the medical data is represented in the matrices $A, B, ..., F$ and the initial value $x_0$ . Depending on the choice of those parameters we get a variety of different model results represented by different curves.

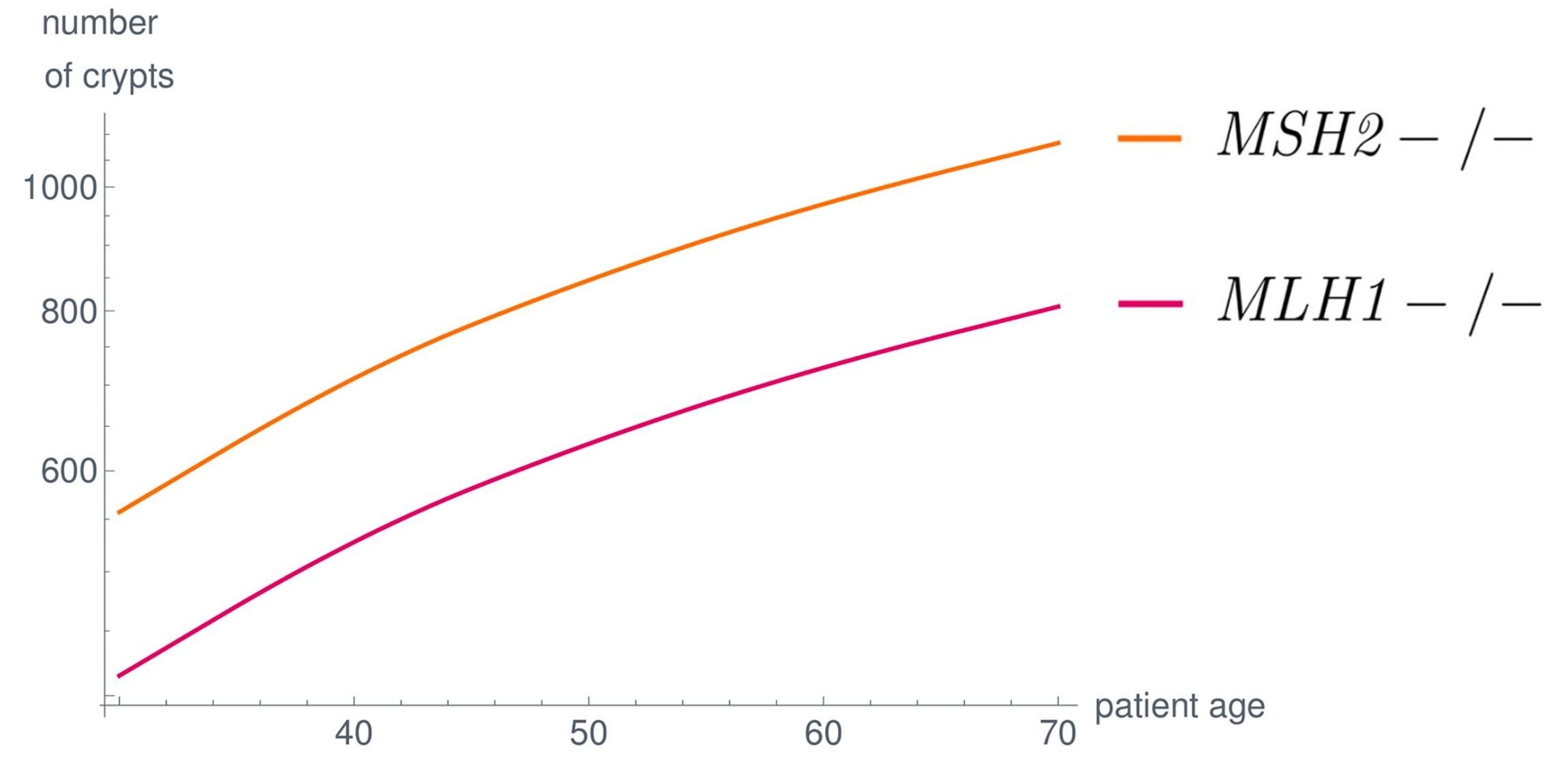
A classical mathematical model results in a deterministic result, i.e., curves with no uncertainty.

Now there is a variety of medical data we use in the model, but we do not know exactly. For example, we assume that cell divisions will take one day, but we also know that not all cells will divide in exactly 24 hours. Similarly, we assume that each crypt has 1500 cells that can divide as a mean value, although there is certainly a lot of variability in this cell count.

We can now describe these uncertainties by defining how likely a cell is to the divide in only 20 hours and setting a probability for cell divisions that take 30 hours. For the other medical data we can model the uncertainties accordingly, or decide to only consider the deterministic mean value.

With deterministic data (left) we state that the cell division takes exactly 24 hours which is often an appropriate approximation but certainly does not capture the entire reality. Uncertain data (middle and right) can describe this variability. Depending on the data at hand we have to decide how uncertain the data is. For data we do not know much about, we choose a larger variance, whereas more precise data with low variance is closer to the deterministic situation.

Once we have a description of the uncertainty in the medical data we can use the mathematical field of uncertainty quantification to model the effect of these data uncertainties on the model results. This will not only give us the deterministic results as mean value but also enables us to make statement on how likely other outcomes are. In plots this often visualized as shaded areas around the deterministic solid lines.

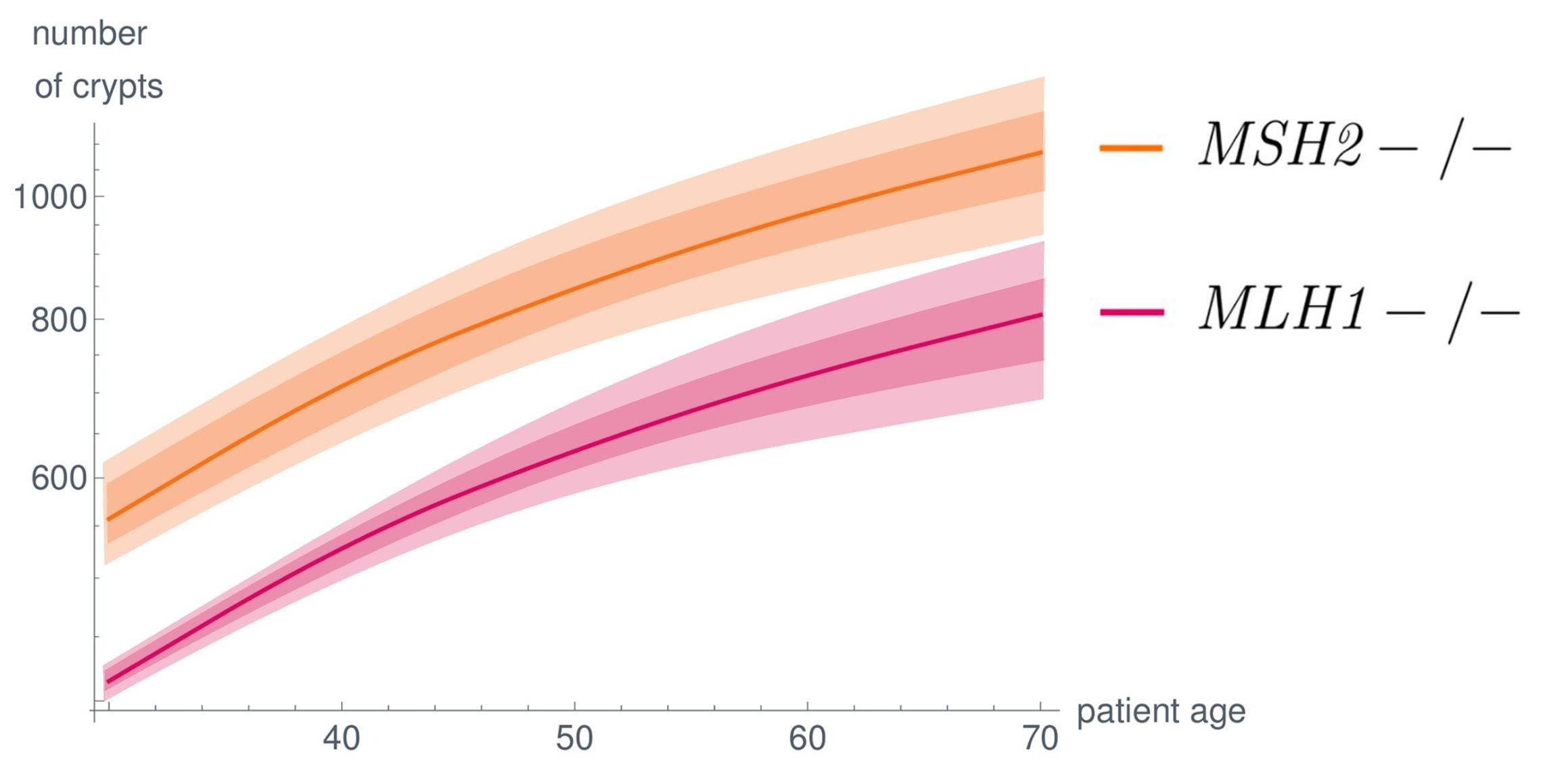
Uncertainty quantification not only gives the deterministic result as a mean value, but also gives the probabilities of slightly lower or higher outcomes.

Uncertainty quantification is helpful in answering many questions

To summarize, uncertainty quantification is helpful in answering many questions. For example, is there any relationship between some medical data and an outcome? Does changing a parameter a little influence the outcome also only a little or a lot? This can also give us indications whether it is really necessary to determine certain biomedical parameters. Alternatively, we can also go in the opposite direction and ask which medical data influences a given outcome the most.

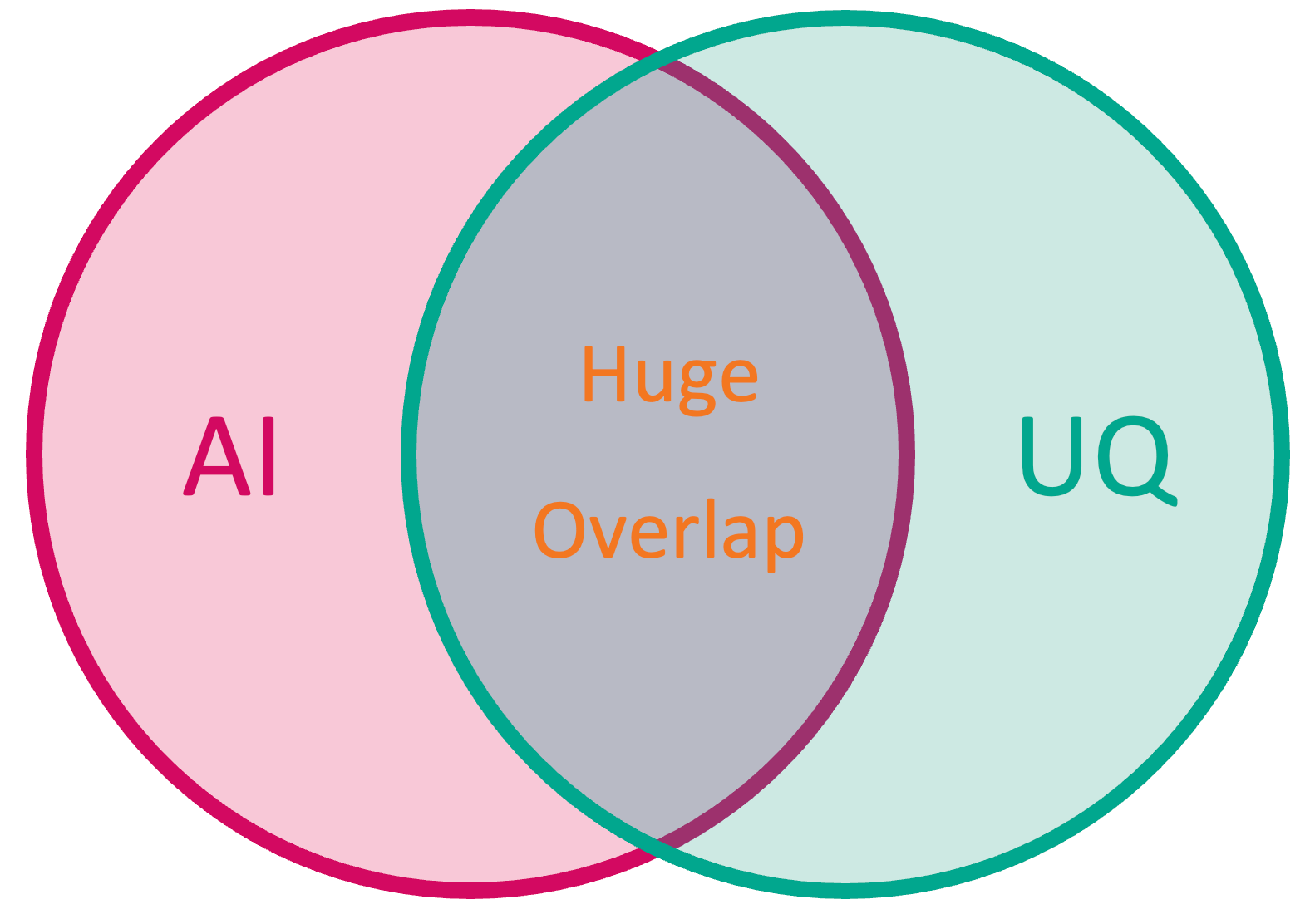
Artificial Intelligence (AI) and Uncertainty Quantification (UQ)

Especially the last point might remind you of another novel approach making its way into oncology: artificial intelligence or machine learning. And indeed, many mathematical techniques found in artificial intelligence can also be found in uncertainty quantification and vice versa. However, it is not necessary to use artificial intelligence in order to apply uncertainty quantification. UQ can also be used in conjunction with more classical mathematical modeling, for example models based on ordinary differential equations.

Don't (unnecessarily) increase the uncertainties

A first step in reducing the uncertainties in clinical decision making is to not increase them unnecessarily by accident. As a general rule of thumb we can say that having more data is beneficial, as we can describe the uncertainties more precisely and thus reduce them. Another point is, that we should do as little as possible preprocessing. Rounding, truncating and clustering data always destroys information we could otherwise use in the data analysis.

While we are on the topic of preprocessing the data: pseudonymization does not increase the uncertainties in any way, so you should always do this!

Conclusion

Let me conclude by saying that uncertainty quantification is extremely useful and important. If you are a mathematical oncologist I encourage you to always consider the uncertainties in the medical and quantify their influence on the results of your mathematical models. On the other hand for the readers of this blog post and the audience of my talk that are clinicians I want to emphasize that uncertainty quantification in mathematical modeling can reduce the uncertainties in clinical decision making you might have.

Original Abstract

In my original abstract for my EHTG conference talk titled “Uncertainty quantification in oncology - How do uncertain data influence model results and clinical decision making?” I wrote:

Uncertainty in medical data is a common challenge in cancer research as many measurements cannot be determined precisely due to experimental restrictions, measurement errors or ethical guidelines. Even more, other parameters may not be measured at all. However, current research results and clinical guidelines heavily rely on data. Thus, quantifying these uncertainties and estimating the impact on cancer outcome and clinical procedures are essential for profound cancer research.
This is true for any kind of cancer research but is analytically feasible in particular when using mathematical models as considered in the fast growing field of mathematical oncology. Here, the aim is to support the clinician by describing medical phenomena through mathematical equations that cannot be observed in vivo. By using state-of-the-art mathematical techniques, we are able to adequately incorporate the data uncertainties in the computations and by this, reflect these in the simulation results.
In the presentation, using the mathematical Kronecker model (Haupt et al., 2021) of the three main pathways (Ahadova et al., 2018) of Lynch syndrome colorectal carcinogenesis, we explain why a sensible modeling of uncertainties is essential and should be considered for any mathematical model in cancer research and beyond. We will discuss common sources and types of data uncertainty and how we can represent them in mathematical computations. Using examples from carcinogenesis modeling, we explain how these uncertainties can be propagated in order to get a reliable quantification of the uncertainties in the model results. Finally, we will give a few recommendations from a mathematical side on medical and clinical data acquisition and processing that support the uncertainty quantification of mathematical models in cancer research.

References

Ahadova, A., Gallon, R., Gebert, J., Ballhausen, A., Endris, V., Kirchner, M., Stenzinger, A., Burn, J., von Knebel Doeberitz, M., Bläker, H., & Kloor, M. (2018). Three Molecular Pathways Model Colorectal Carcinogenesis in Lynch Syndrome: Three Pathways of CRC in Lynch Syndrome. International Journal of Cancer, 143(1), 139–150. https://doi.org/10.1002/ijc.31300

Haupt, S., Zeilmann, A., Ahadova, A., Bläker, H., von Knebel Doeberitz, M., Kloor, M., & Heuveline, V. (2021). Mathematical modeling of multiple pathways in colorectal carcinogenesis using dynamical systems with Kronecker structure. PLOS Computational Biology, 17(5), e1008970. https://doi.org/10.1371/journal.pcbi.1008970